ellipsoidische Höhe - GeoLexikon

fast ausschliesslich verwendete geometrische Höhe, die den Abstand eines Raumpunktes längs eines geradlinigen Lotes von einem geeignet gewählten Rotationsellipsoid angibt. Ellipsoidische Höhen können im Prinzip mit Hilfe der trigonometrischen Höhenbestimmung (unter Berücksichtigung der Lotabweichungen) bzw. des trigonometrischen Nivellements oder alternativ mit Hilfe des geometrisch-astronomischen Nivellements bestimmt werden. Diese Verfahren sind nur mässig genau und sehr aufwendig. Neuerdings können ellipsoidische Höhen mit Hilfe präziser Navigationsverfahren (z.B. GPS) verhältnismässig schnell gemessen und bei Kenntnis des Geoides bzw. des Quasigeoides in physikalische Höhen, wie z.B. in orthometrische Höhen bzw. Normalhöhen umgerechnet werden. Diese Vorgehensweise wird zunehmend zur Bestimmung von physikalisch definierten metrischen Höhen angewendet, auch wenn die Genauigkeit noch hinter der des geodätischen Nivellements zurückbleibt. Der Ortsvektor
eines beliebigen Raumpunktes P kann als Summe des Ortsvektors
_E zum Ellipsoid-Projektionspunkt P_E und dem Normalenvektor
in diesem Punkt, multipliziert mit der ellipsoidischen Höhe h, dargestellt werden (Abb. 1):

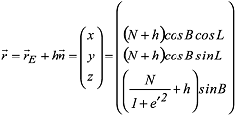mit der ellipsoidischen Breite B, der ellipsoidischen Länge L (ellipsoidische Koordinaten) sowie dem Querkrümmungshalbmesser N und der zweiten numerischen Exzentrizität e' (Rotationsellipsoid). Die Berechnung von ellipsoidischer Länge L, Breite B und Höhe h aus den rechtwinklig kartesischen Koordinaten erhält man in folgenden Schritten. Die Länge ergibt sich direkt aus der Formel:

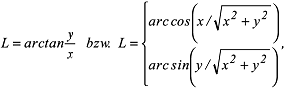während die Breite B iterativ berechnet werden muss. Man beginnt die Iteration mit der Breite unter Vernachlässigung der ellipsoidischen Höhe

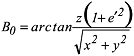und führt die in Abbildung 2 aufgeführten Rechenschritte iterativ aus.

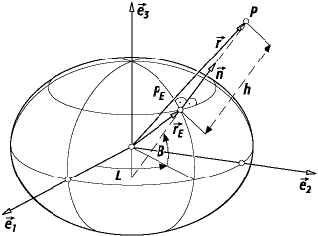ellipsoidische Höhe 1: ellipsoidische Höhe h eines Punktes P, gemessen von der Oberfläche des Rotationsellipsoides (P = Raumpunkt, P_E = Ellipsoid-Projektionspunkt, L = ellipsoidische Länge, B = ellipsoidische Breite, = Ortsvektor,

_E = Summe

des Ortsvektors,

= Normalenvektor, h = ellipsoidische Höhe,

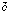
₁,
₂,
₃ = globales geodätisches Koordinatensystem).

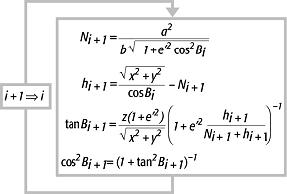ellipsoidische Höhe 2: iterative Berechnung der ellipsoidischen Höhe aus den rechtwinklig kartesischen Koordinaten.