ru.wikipedia.org

Квадратное уравнение — Википедия

Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом

$ax^{2}+bx+c=0,\;a\neq 0,$

в котором $x$ — неизвестное, а коэффициенты $a$ , $b$ и $c$ — вещественные или комплексные числа.

Выражение ax² + bx + c называется квадратным трёхчленом. Корень уравнения $ax^{2}+bx+c=0$ — это значение неизвестного $x$ , обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство. Также это значение называется корнем самого многочлена $ax^{2}+bx+c$ .

Элементы квадратного уравнения имеют собственные названия^[1]:

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице^[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент $a$ :

$x^{2}+px+q=0,\quad p={\dfrac {b}{a}},\quad q={\dfrac {c}{a}}.$

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.

Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения^[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:

$x^{2}+x={\frac {3}{4}};\ x^{2}-x=14{\frac {1}{2}}.$

Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанном индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)^[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: $ax^{2}+bx=c;$ притом предполагалось, что в нём все коэффициенты, кроме $a,$ могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.

I способ. Общая формула для вычисления корней с помощью дискриминанта

[править | править код]

Дискриминантом квадратного уравнения $ax^{2}+bx+c=0$ называется величина ${\mathcal {D}}=b^{2}-4ac$ .

Условие	${\mathcal {D}}>0$	${\mathcal {D}}=0$	${\mathcal {D}}<0$
Количество корней	Два корня	Один корень кратности 2 (другими словами, два равных корня)	Действительных корней нет
Формула	$x_{1,2}={\frac {-b\pm {\sqrt {\mathcal {D}}}}{2a}}$ (1)	$x=-{\frac {b}{2a}}$	—

Следствия:

Данный метод универсальный, однако не единственный.

Для уравнений вида $ax^{2}+2kx+c=0$ , то есть при чётном $b$ , где

$k={\dfrac {1}{2}}b,$

вместо формулы (1) для нахождения корней существует возможность использования более простых выражений^[1].

Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b = 2k, через несложные преобразования.

Дискриминант	Корни
неприведённое	приведённое	D > 0	неприведённое	приведённое
удобнее вычислять значение четверти дискриминанта: ${\dfrac {\mathcal {D}}{4}}=k^{2}-ac$ Все необходимые свойства при этом сохраняются.	${\dfrac {\mathcal {D}}{4}}=k^{2}-c$ .	$x_{1,2}={\dfrac {-k\pm {\sqrt {k^{2}-ac}}}{a}}.$	$x_{1,2}=-k\pm {\sqrt {k^{2}-c}}$
D = 0	$x={\dfrac {-k}{a}}$	$x=-k$

К решению неполных квадратных уравнений практикуется особый подход. Рассматриваются три возможных ситуации.

Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту

[править | править код]

Если в квадратном уравнении $ax^{2}+bx+c=0$ сумма первого коэффициента и свободного члена равна второму коэффициенту: $a+c=b$ , то его корнями являются $-1$ и число, противоположное отношению свободного члена к старшему коэффициенту ( $-{\frac {c}{a}}$ ).

Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):

${\mathcal {D}}=b^{2}-4ac=(a+c)^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}$ .

Да, это так, ведь при любых действительных значениях коэффициентов $(a-c)^{2}\geqslant 0$ , а значит и дискриминант неотрицателен. Таким образом, если $a\not =c$ , то уравнение имеет два корня, если же $a=c$ , то оно имеет только один корень. Найдём эти корни:

$x_{1,2}={\frac {-b\pm {\sqrt {\mathcal {D}}}}{2a}}={\frac {-(a+c)\pm {\sqrt {(a-c)^{2}}}}{2a}}={\frac {-a-c\pm |a-c|}{2a}}={\frac {-a-c\pm a\mp c}{2a}}$ .

$x_{1}={\frac {-a-c-a+c}{2a}}={\frac {-2a}{2a}}=-1;$

$x_{2}={\frac {-a-c+a-c}{2a}}={\frac {-2c}{2a}}=-{\frac {c}{a}}.$

В частности, если $a=c$ , то корень будет один: $-1.$

Способ 2 [геометрический].

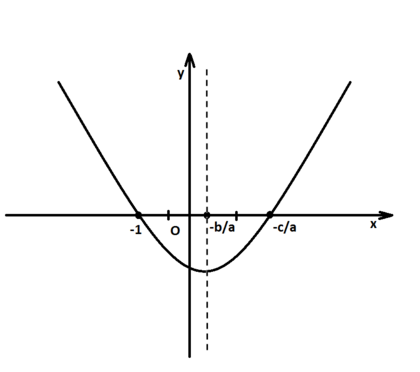
Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы $y=ax^{2}+bx+c$ с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой $x=-{\frac {b}{2a}}$ . Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: $-{\frac {b}{2a}}+\rho (x_{1};-{\frac {b}{2a}})=x_{2}$ (если $x_{1}<x_{2}$ ) или $-{\frac {b}{2a}}-\rho (-{\frac {b}{2a}};x_{1})=x_{2}$ (если верно неравенство противоположного смысла). Используя тождество $\rho (a;b)=|a-b|$ , выражающее геометрический смысл модуля, а также принимая, что $x_{1}=-1$ (это можно доказать, подставив равенство в квадратный трёхчлен: $a\cdot (-1)^{2}+b\cdot (-1)+c=(a+c)-b=0$ , поэтому -1 - корень такого уравнения) , приходим к следующему равенству: $-{\frac {b}{2a}}\pm |-{\frac {b}{2a}}-(-1)|=x_{2}.$ Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем - отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве $b-a=c$ , раскрываем модуль: $x_{2}=-{\frac {b}{2a}}-{\frac {b}{2a}}+1=-{\frac {2b-2a}{2a}}=-{\frac {b-a}{a}}=-{\frac {c}{a}}$ . Во втором случае, совершив аналогичные преобразования, придём к тому же результату, ч. т. д.

Способ 3 [разложение на множители].

Совершим подстановку условия $a+c=b$ в уравнение $ax^{2}+bx+c=0$ . Тогда $ax^{2}+(a+c)x+c=0\Longleftrightarrow ax(x+1)+c(x+1)=0\Longleftrightarrow (x+1)(ax+c)=0.$ Откуда $x=-1$ либо $x=-{\frac {c}{a}}$ .

Способ 4 [эвристический]. Применим следующее соображение: «Если для объектов $A$ , $B$ и $C$ найдутся такие ненулевые числа $\alpha$ и $\beta$ , что выполняется равенство $\alpha A+\beta B=\left(\alpha +\beta \right)C$ , тогда $A=B=C$ либо же ${\frac {\alpha }{\beta }}={\frac {C-B}{A-C}}$ ( $\alpha \neq \beta$ )», в истинности которого несложно убедиться. Уравнение $ax^{2}+bx+c=0$ представим в виде $ax^{2}+cx^{0}=b(-x^{1})$ . С учётом того, что $a+c=b$ и написанного выше, делаем вывод: $x^{2}=x^{0}=-x^{1}$ , или, что то же самое, $x=-x^{0}=-1$ . Второй (отличный от этого) корень ищется по формуле ${\frac {x^{2}-(-x)}{-x-1}}={\frac {c}{a}}$ . Применяя основное свойство дроби ( $x\neq -1$ ) и свойство алгебраического равенства (умножение на $-1$ ), получим требуемый результат: $x=-{\frac {c}{a}}$ .

Отсюда следует, что перед решением какого-либо квадратного уравнения целесообразна проверка возможности применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю

[править | править код]

Если в квадратном уравнении сумма всех его коэффициентов равна нулю ( $a+b+c=0$ ), то корнями такого уравнения являются $1$ и отношение свободного члена к старшему коэффициенту ( ${\frac {c}{a}}$ ).

Способ 1. Прежде всего заметим, что из равенства $a+b+c=0$ следует, что $b=-(a+c)$ Установим количество корней:

${\mathcal {D}}=b^{2}-4ac=(-(a+c))^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}.$

При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов $(a-c)^{2}\geqslant 0$ , а значит и дискриминант неотрицателен. Обратите внимание, что если $a\not =c$ , то уравнение имеет два корня, если же $a=c$ , то только один. Найдём эти корни:

$x_{1,2}={\frac {-b\pm {\sqrt {\mathcal {D}}}}{2a}}={\frac {a+c\pm {\sqrt {(a-c)^{2}}}}{2a}}={\frac {a+c\pm |a-c|}{2a}}={\frac {a+c\pm a\mp c}{2a}};$

$x_{1}={\frac {a+c+a-c}{2a}}={\frac {2a}{2a}}=1;$

$x_{2}={\frac {a+c-a+c}{2a}}={\frac {2c}{2a}}={\frac {c}{a}},$

что и требовалось доказать.

В частности, если $a=c$ , то уравнение имеет только один корень, которым является число $1$ .

Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: $a\cdot 1^{2}+b\cdot 1+c=0$ - верное равенство, следовательно, единица - корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту - $x_{1}x_{2}={\frac {c}{a}}\Rightarrow x_{2}={\frac {c}{ax_{1}}}={\frac {c}{a\cdot 1}}={\frac {c}{a}}$ , ч.т.д.

Отсюда следует, что перед решением уравнения стандартными методами целесообразна проверка применимости к нему этой теоремы, а именно сложение всех коэффициентов данного уравнения и установление, не равна ли нулю эта сумма.

Если трёхчлен вида $ax^{2}+bx+c~(a\not =0)$ удастся каким-либо образом представить в качестве произведения линейных множителей $(kx+m)(lx+n)=0$ , то можно найти корни уравнения $ax^{2}+bx+c=0$ — ими будут $-{\frac {m}{k}}$ и $-{\frac {n}{l}}$ , действительно, ведь $(kx+m)(lx+n)=0\Longleftrightarrow {\biggl [}{\begin{array}{lcl}kx+m=0,\\lx+n=0,\end{array}}$ а решив указанные линейные уравнения, получим вышеописанное. Квадратный трёхчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.

Рассматриваются некоторые частные случаи.

Если квадратный трёхчлен имеет вид $(ax)^{2}+2abx+b^{2}$ , то применив к нему названную формулу, можно разложить его на линейные множители и, значит, найти корни:

$(ax)^{2}+2abx+b^{2}=(ax+b)^{2},$

$(ax+b)^{2}=0,$

$x=-{\frac {b}{a}}.$

Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:

прибавляют и отнимают одно и то же число:
$x^{2}+px+({\frac {p}{2}})^{2}-({\frac {p}{2}})^{2}+q=0;$ .
применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть:
$(x^{2}+2{\frac {p}{2}}x+({\frac {p}{2}})^{2})+(-({\frac {p}{2}})^{2}+q)=0,$
$(x+{\frac {p}{2}})^{2}={\frac {p^{2}}{4}}-q;$
извлекают из левой и правой частей уравнения квадратный корень и выражают переменную:
$x+{\frac {p}{2}}=\pm {\sqrt {{\frac {p^{2}}{4}}-q}},$
$x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}.$

Примечание: данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a = 1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.

Прямая теорема Виета (см. ниже) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).

Согласно обратной теореме, всякая пара чисел (число) $x_{1},x_{2}$ , будучи решением системы уравнений

${\begin{cases}x_{1}+x_{2}=-p,\\x_{1}x_{2}=q,\end{cases}}$

являются корнями уравнения $x^{2}+px+q=0$ .

Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:

1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;

2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.

По своей сущности метод «переброски» является просто модификацией теоремы Виета.

Метод «переброски» — это сведение уравнения, которое нельзя привести так, чтобы все коэффициенты остались целыми, к приведённому уравнению с целыми коэффициентами:

1) умножаем обе части на старший коэффициент:

$ax^{2}+bx+c=0\quad \mid \;\cdot a,$

$(ax)^{2}+b(ax)+ac=0;$

2) заменяем $y=ax\colon$

$y^{2}+by+ac=0.$

Далее решаем уравнение относительно $y$ по методу, описанному выше, и находим $x={\dfrac {y}{a}}$ .

$5x^{2}-26x+5=0,$

${\begin{cases}x={\dfrac {y}{5}},\\y^{2}-26y+25=0;\end{cases}}$

Сумма коэффициентов при степенях введённого неизвестного $y$ равна нулю, поэтому

$y_{1}=1,\quad y_{2}=25.$

Возвращаемся к «старой» переменной:

$x_{1}={\dfrac {1}{5}},\quad x_{2}=5.$

Ответ: $\left\{{\dfrac {1}{5}};\;5\right\}$ .

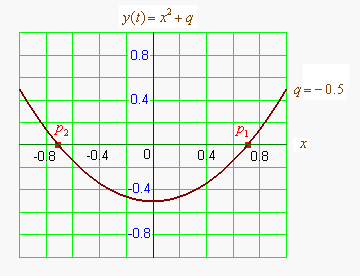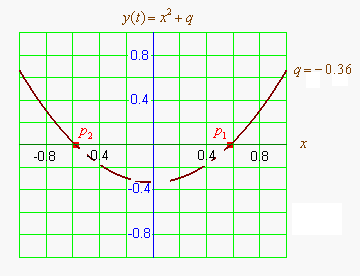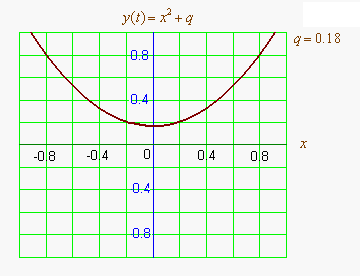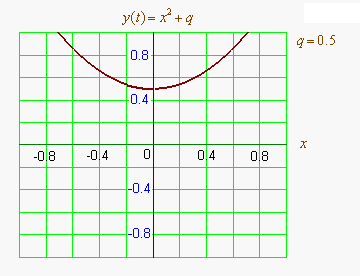
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)

Если коэффициент $a$ положительный, ветви параболы направлены вверх и наоборот. Если коэффициент $b$ положительный (при положительном $a$ , при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.

Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида $f(x)=g(x)$ заключается в следующем: в одной системе координат строят графики функций $y=f(x)$ и $y=g(x)$ и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.

Есть всего пять основных способов графического решения квадратных уравнений.

Для решения квадратного уравнения $ax^{2}+bx+c=0$ строится график функции $y=ax^{2}+bx+c$ и отыскиваются абсциссы точек пересечения такого графика с осью $x$ .

Для решения того же уравнения этим приёмом уравнение преобразуют к виду $ax^{2}=-bx-c$ и строят в одной системе координат графики квадратичной функции $y=ax^{2}$ и линейной функции $y=-bx-c$ , затем находят абсциссу точек их пересечения.

Данный приём подразумевает преобразование исходного уравнения к виду $a(x+l)^{2}+m=0$ , используя метод выделения полного квадрата суммы (разности) и затем в $a(x+l)^{2}=-m$ . После этого строятся график функции $y=a(x+l)^{2}$ (им является график функции $y=ax^{2}$ , смещённый на $|l|$ единиц масштаба вправо или влево в зависимости от знака) и прямую $y=-m$ , параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.

Квадратное уравнение преобразуют к виду $ax^{2}+c=-bx$ , строят график функции $y=ax^{2}+c$ (им является график функции $y=ax^{2}$ , смещённый на $c$ единиц масштаба вверх, если этот коэффициент положителен, либо вниз, если он отрицателен), и $y=-bx$ , находят абсциссы их общих точек.

Квадратное уравнение преобразуют к особому виду:

${\dfrac {ax^{2}}{x}}+{\dfrac {bx}{x}}+{\dfrac {c}{x}}={\dfrac {0}{x}};$

$ax+b+{\dfrac {c}{x}}=0;$

затем

$ax+b=-{\dfrac {c}{x}}.$

Совершив преобразования, строят графики линейной функции $y=ax+b$ и обратной пропорциональности $y=-{\frac {c}{x}};\ (c\not =0)$ , отыскивают абсциссы точек пересечения этих графиков. Этот приём имеет границу применимости: если $c=0$ , то приём не используется.

Описанные выше приёмы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.

Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.

Построить в системе координат $Oxy$ окружность с центром в точке $S\left(-{\dfrac {b}{2a}};{\dfrac {a+c}{2a}}\right)$ , пересекающую ось $Oy$ в точке $C\left(0;\,1\right)$ .
Далее возможны три случая:

Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки $A(x_{1};0),B(x_{2};0),C(0;1)$ , где $x_{1},x_{2}$ , естественно, действительные корни квадратного уравнения (подчёркиваем: если они имеются). Найдём координаты центра такой окружности. Для этого докажем, что эта окружность проходит через точку $D(0;{\frac {c}{a}})$ . Действительно, согласно теореме о секущих, в принятых обозначениях выполняется равенство $OA\cdot OB=OC\cdot OD$ (см рисунок). Преобразовывая это выражение, получаем величину отрезка OD, которой и определяется искомая ордината точки D: $OD={\dfrac {OA\cdot OB}{OC}}={\frac {x_{1}x_{2}}{1}}={\frac {c}{a}}$ (в последнем преобразовании использована теорема Виета (см. ниже в одноимённом разделе)). Если же корень один, то есть ось абсцисс будет касательной к такой окружности, и окружность пересекает ось y в точке с ординатой 1, то она обязательно пересечёт её и в точке с указанной выше ординатой (в частности, если 1=c/a, это могут быть совпадающие точки), что доказывается аналогично с использованием уже теоремы о секущей и касательной, являющаяся частным случаем теоремы о секущих. В первом случае ( ${\dfrac {c}{a}}\not =1$ ), определяющими будут точка касания, точка оси y с ординатой 1, и её же точка с ординатой ${\dfrac {c}{a}}$ . Если c/a и 1 - совпадающие точки, а корня два, определяющими будут эта точка и точки пересечения с осью абсцисс. В случае, когда (1=c/a) и корень один, указанных сведений достаточно для доказательства, так как такая окружность может быть только одна - её центром будет вершина квадрата, образуемого отрезками касательных и перпендикулярами, а радиус - стороне этого квадрата, составляющей 1. Пускай S - центр окружности, имеющей с осью абсцисс две общие точки. Найдём его координаты: для этого опустим от этой точки перпендикуляры к координатным осям. Концы этих перпендикуляров будут серединами отрезков AB и CD - ведь треугольники ASB и CSD равнобедренные, так как в них AS=BS=CS=DS как радиусы одной окружности, следовательно, высоты в них, проведённые к основаниям, также являются и медианами. Найдём координаты середин названных отрезков. Так как парабола симметрична относительно прямой $x=-{\dfrac {b}{2a}}$ , то точка этой прямой с такой же абсциссой будет являться серединой отрезка AB. Следовательно, абсцисса точки S равна этому числу. В случае же, если уравнение имеет один корень, то ось x является касательной по отношению к окружности,поэтому, согласно её свойству, её радиус перпендикулярен оси, следовательно, и в этом случае указанное число - абсцисса центра. Её ординату найдём так: ${\dfrac {CD}{2}}={\dfrac {OC+(OC+CD)}{2}}={\dfrac {OC+OD}{2}}={\dfrac {1+{\dfrac {c}{a}}}{2}}={\dfrac {a+c}{2a}}$ . В третьем из возможных случаев, когда c\a=1 (и, значит, a=c), то ${\dfrac {c}{a}}=1={\dfrac {2a}{2a}}={\dfrac {a+c}{2a}}$ .

Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке $S(-{\dfrac {b}{2a}};{\dfrac {c+a}{2a}})$ , проходящую через точку $C(0;1)$ , то она, в случаях, когда уравнение имеет действительные корни, пересечёт ось x в точках, абсциссы которых есть эти корни. Причём, если длина радиуса больше длины перпендикуляра к оси Ox, то уравнение имеет два корня (предположив обратное, мы бы получили противоречие с доказанным выше), если длины равны, то один (по той же причине), если же длина радиуса меньше длины перпендикуляра, то окружность не имеет общих точек с осью x, следовательно, и действительных корней у уравнения нет (доказывается тоже от противного: если корни есть, то окружность, проходящая через A, B, C совпадает с данной, и поэтому пересекает ось, однако она не должна пересекать ось абсцисс по условию, значит, предположение неверно).

Квадратное уравнение с вещественными коэффициентами $a,~b,~c$ всегда имеет с учётом кратности два комплексных корня, о чём гласит основная теорема алгебры. При этом, в случае неотрицательного дискриминанта корни будут вещественными, а в случае отрицательного — комплексно-сопряжёнными:

В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два корня единичной кратности).

Квадратное уравнение вида $x^{2}+px+q=0,$ в котором старший коэффициент $a$ равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до

$x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}.$

Мнемонические правила:

Из «Радионяни»:

«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное^[2] q.

Из «Радионяни» (второй вариант):

p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.

Из «Радионяни» (третий вариант на мотив Подмосковных вечеров):

Чтобы x найти к половине p,
Взятой с минусом не забудь,
Радикал приставь с плюсом минусом,
Аккуратно, не как-нибудь.
А под ним квадрат половины p,
Ты, убавь на q и конец,
Будет формула приведенная,
Рассуждений твоих венец.
Будет формула приведенная,
Рассуждений твоих венец.

Основная статья: Теорема Виета

Сумма корней приведённого квадратного уравнения $x^{2}+px+q=0$ (вещественных или комплексных) равна второму коэффициенту $p$ , взятому с противоположным знаком, а произведение этих корней — свободному члену $q$ :

$x_{1}+x_{2}=-p,\quad x_{1}x_{2}=q.$

С его помощью приведённые уравнения можно решать устно:

В общем случае, то есть для неприведённого квадратного уравнения $ax^{2}+bx+c=0\colon$

${\begin{cases}x_{1}+x_{2}=-b/a,\\x_{1}x_{2}=c/a.\end{cases}}$

На практике (следуя методу «переброски») для вычисления корней применяется модификация теорема Виета:

${\begin{cases}x_{1}+x_{2}=-b/a&\mid \cdot a,\\x_{1}x_{2}=c/a&\mid \cdot a^{2};\end{cases}}$

${\begin{cases}(ax_{1})+(ax_{2})=-b,\\(ax_{1})(ax_{2})=ac,\end{cases}}$

по которой можно устно находить ax₁, ax₂, а оттуда — сами корни:

Но у некоторых неприведённых уравнений корни можно устно угадать даже по стандартной теореме Виета:

Разложение квадратного трёхчлена на множители и теоремы, следующие из этого

[править | править код]

Если известны оба корня квадратного трёхчлена, его можно разложить по формуле

$ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$ (2)

Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни $x_{1}$ и $x_{2}$ квадратного уравнения $ax^{2}+bx+c=0$ образуют соотношения с его коэффициентами: $x_{1}+x_{2}=-{\frac {b}{a}},\ x_{1}x_{2}={\frac {c}{a}}$ . Подставим эти соотношения в квадратный трёхчлен:

${\begin{alignedat}{2}ax^{2}+bx+c&=a(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}})=a(x^{2}-(x_{1}+x_{2})x+x_{1}x_{2})=\\&=a(x^{2}-x_{1}x-x_{2}x+x_{1}x_{2})=a(x(x-x_{1})-x_{2}(x-x_{1}))\\&=a(x-x_{1})(x-x_{2}).\end{alignedat}}$

В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Из формулы (2) имеются два важных следствия:

Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.

Пусть $ax^{2}+bx+c=(kx+m)(nx+l)$ . Тогда, переписав это разложение, получим:

$(kx+m)(nx+l)=k(x+{\frac {m}{k}})n(x+{\frac {l}{n}})=kn(x-(-{\frac {m}{k}}))(x-(-{\frac {l}{n}}))$ .

Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются $-{\frac {m}{k}}$ и $-{\frac {l}{n}}$ . Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества $\mathbb {R}$ .

Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.

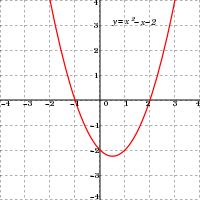
Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве $\mathbb {R}$ , что противоречит условию, а потому наше предположение неверно, и такой трёхчлен не раскладывается на линейные множители.

Для квадратичной функции:
f (x) = x² − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось абсцисс, x = −1 и x = 2, являются решениями квадратного уравнения: x² − x − 2 = 0.

Уравнение вида $a\cdot f^{2}(x)+b\cdot f(x)+c=0$ является уравнением, сводящимся к квадратному.

В общем случае оно решается методом введения новой переменной, то есть заменой $f(x)=t,~t\in {\mathcal {E}}(f),$ где ${\mathcal {E}}$ — множество значений функции $f$ , c последующим решением квадратного уравнения $a\cdot t^{2}+b\cdot t+c=0$ .

Также при решении можно обойтись без замены, решив совокупность двух уравнений:

$f(x)={\frac {-b-{\sqrt {b^{2}-4\cdot a\cdot c}}}{2a}}$ и

$f(x)={\frac {-b+{\sqrt {b^{2}-4\cdot a\cdot c}}}{2a}}$

К примеру, если $f(x)=x^{2}$ , то уравнение принимает вид:

$ax^{4}+bx^{2}+c=0.$

Такое уравнение 4-й степени называется биквадратным^[4]^[1].

С помощью замены

$y=x+{\dfrac {k}{x}}$

к квадратному уравнению сводится уравнение

$ax^{4}+bx^{3}+cx^{2}+kbx+k^{2}a=0,$

известное как возвратное или обобщённо-симметрическое уравнение^[1].

Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка

$y''+py'+qy=0$

подстановкой $y=e^{kx}$ сводится к характеристическому квадратному уравнению:

$k^{2}+pk+q=0$

Если решения этого уравнения $k_{1}$ и $k_{2}$ не равны друг другу, то общее решение имеет вид:

$y=Ae^{k_{1}x}+Be^{k_{2}x}$ , где $A$ и $B$ — произвольные постоянные.

Для комплексных корней $k_{1,2}=k_{r}\pm k_{i}i$ можно переписать общее решение, используя формулу Эйлера:

$y=e^{k_{r}x}\left(A\cos {k_{i}x}+B\sin {k_{i}x}\right)=Ce^{k_{r}x}\cos(k_{i}x+\varphi ),$

где A, B, C, φ — любые постоянные. Если решения характеристического уравнения совпадают $k_{1}=k_{2}=k$ , общее решение записывается в виде:

$y=Axe^{kx}+Be^{kx}$

Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.

Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.

Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом Архивная копия от 28 января 2016 на Wayback Machine / Фестиваль педагогических идей «Открытый урок».
Математические методы